Bài 1
(3 điểm)
1) Giải phương trình
\[ \sqrt{x+1}+\sqrt{1-x}+\sqrt{1-x^2}=3 \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} 3 x^2+2 y^2+7 x y=12 \\ x^3+3 x^2 y+2 y^2 x+2 x+4 y=12 \end{array}\right. \]
Cách giải 1:
1) Đặt \(t=\sqrt{x+1}+\sqrt{1-x} \rightarrow t^2=2+2 \sqrt{1-x^2}\) với \( t \gt 0\)
\(\rightarrow \sqrt{1-x^2}=\dfrac{t^2-2}{2}\). Thay vào phương trình ban đâu ta có \(t+\dfrac{t^2-2}{2}=3\)
\(\leftrightarrow t^2+2 t-8=0 \leftrightarrow(t-2)(t+4)=0 \leftrightarrow t=2\)
Thu được
\(\sqrt{x+1}+\sqrt{1-x}=2 \leftrightarrow 2 \sqrt{1-x^2}+2=4\)
\(\leftrightarrow \sqrt{1-x^2}=1 \leftrightarrow 1-x^2=1 \leftrightarrow x=0\).
Vậy phương trình có nghiệm \(x=0\).
2) Hệ phương trình tương dương với
\[ \left\{\begin{array}{l} (x+2 y)(3 x+y)=12 \\ (x+2 y)\left(x^2+x y+2\right)=12 \end{array}\right. \]
suy ra \(x^2+x y+2=3 x+y\)
\(\leftrightarrow x(x+y)+2=(x+y)+2 x\)
\(\leftrightarrow(x-1)(x+y-2)=0\)
- Giải \(\left\{\begin{array}{l}x=1 \\ (2 y+1)(y+3)=12 \rightarrow 2 y^2+7 y-9=0 \rightarrow y=1, y=-\dfrac{9}{2}\end{array}\right.\)
- Giải \(\left\{\begin{array}{l}x+y=2 \\ (y+2)(6-2 y)=12 \leftrightarrow(y+2)(3-y)=6 \leftrightarrow y^2-y=0 \leftrightarrow y=0, y=1\end{array}\right.\)
Bài 2
(3 điểm)
1) Tìm \(x, y\) nguyên thỏa mān
\[ y=\dfrac{x+1}{x^4+1} \]
2) Với \(a, b, c\) là những số thực dương thỏa mãn \(a b+b c+c a=1\). Tìm giá trị nhỏ nhất của biểu thức
\[ P=2 a^2+b^2+c^2 \]
Cách giải 1:
1) Suy ra \(x^4+1\left|x+1 \rightarrow x^4+1\right|(x+1)(x-1)\left(x^2+1\right)=x^4-1\)
\[ \rightarrow x^4+1\left|\left(x^4+1\right)-2 \rightarrow x^4+1\right| 2 \rightarrow x^4+1 \in\{1,2\} \]
- \(x^4+1=1 \rightarrow x=0 \rightarrow y=1\)
- \(x^4+1=2 \rightarrow x=1, y=1\) hoăc \(x=-1, y=0\).
2) Ta có
\[ \begin{array}{r} \left\{\begin{array}{l} a^2+\alpha^2 b^2 \geq 2 \alpha a b \\ a^2+\alpha^2 c^2 \geq 2 \alpha a c \\ \alpha\left(b^2+c^2\right) \geq 2 \alpha b c \end{array}\right. \\ \rightarrow 2 a^2+\left(\alpha^2+\alpha\right)\left(b^2+c^2\right) \geq 2 \alpha(a b+b c+c a) \end{array} \]
(Đẳng thức xảy \(\mathrm{ra} \leftrightarrow b=c=\frac{1}{\alpha} a\) )
Chọn \(\alpha>0\) là nghiệm của phương trình
\[ \alpha^2+\alpha=1 \leftrightarrow \alpha^2+\alpha-1=0 \rightarrow \alpha=\frac{\sqrt{5}-1}{2} \]
Thay vào (1) ta thu được
\[ 2 a^2+b^2+c^2 \geq \sqrt{5}-1 \rightarrow P_{\text {min }}=\sqrt{5}-1 \quad \text { khi } b=c=\frac{2}{\sqrt{5}-1} a \]
Bài 3
(3 điểm)
Cho hình thang \(A B C D\) nội tiếp đường tròn \((O)\) với \(A D || B C\) và \(A D \lt B C\). Giả sử tam giác \(A B C\) nhọn, không cân. Gọi \(P\) là điểm đối xứng của \(A\) qua \(B C\).
1) Chứng minh rằng \(D P\) đi qua trung điểm \(M\) của \(B C\).
2) Gọi \(K\) là trung điểm \(A P\). Chứng minh rằng \(K D\) đi qua trọng tâm tam giác \(A B C\).
3) Goi \(H\) là trực tâm tam giác \(A B C\). Giả sử có \(F\) nằm trên đường thẳng \(B D\) sao cho \(A F \perp H M\). Chứng minh rằng \(F K, A C, P D\) đồng quy.
Cách giải 1:
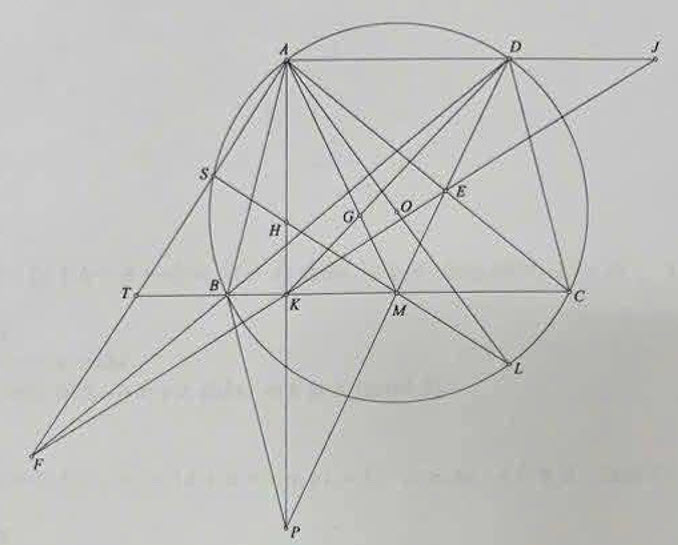
1) ( 1.5 điểm) Dễ thấy \(A B C D\) là hình thang cân. Theo tính chất đối xứng và tính chất hình thang cân thì \(\angle P B C=\angle A B C=\angle D C B\). Từ đó \(P B \| C D\). Mà \(P B=A B=C D\). Từ đó \(D B P C\) là hình bình hành, hay \(P D\) đi qua trung điểm \(M\) của \(B C\).
2) (1.0 điểm) Gọi \(G\) là trọng tâm tam giác \(A B C\) thì \(\frac{G M}{G A}=\frac{1}{2}=\frac{K M}{A D}\). Dẳng thức cuối có do tính chất đường trung bình trong tam giác \(P A D\). Từ đó hai tam giác \(G M K\) và \(G A D\) dồng dạng c.g.c nên \(K, G, D\) thẳng hàng.
3) ( 0.5 điểm) Gọi \(A L\) là đường kính của \((O)\). Dễ thấy \(B H C L\) là hình bì̀nh hành nên \(H L\) đi qua trung điểm \(M\) của \(B C\). Gọi giao điểm thứ hai của \(L H\) và \((O)\) là \(S\). Dễ thấy \(A S \perp H M\) nên \(S\) thuộc \(A F\). (Vì theo giả thiết \(A F \perp H M\) ). Gọi \(T\) là giao điểm của \(A F\) và \(B C\), dễ thấy \(H\) là trực tâm tam giác \(A T M\). Từ đó
\[ K T \cdot K M=K H \cdot K A=K B \cdot K C \]
Hệ quả là
\[ \frac{K T}{K C}=\frac{K B}{K M}=\frac{K T-K B}{K C-K M}=\frac{T B}{M C} \]
Goi \(E\) là giao điển của \(M D\) và \(A C\). Ta sẽ chứng minh \(F, K, E\) thẳng hàng. Thật vậy, gọi giao điểm của \(F K\) với \(A D\) là \(J\), ta đưa về chứng minh \(K, E, J\) thẳng hàng. Sử dụng (1), và định lý Thales ta thấy
\[ \frac{K C}{A J}=\frac{K C}{K T} \cdot \frac{K T}{A J}=\frac{M C}{T B} \cdot \frac{T B}{A D}=\frac{M C}{A D}=\frac{E C}{E A} \]
Đẳng thức (2) kết hợp với \(\angle E C K=\angle E A J\) (do \(C K \| A J\) ) thể hiện hai tam giác \(E C K\) và \(E A J\) đồng dạng (c.g.c) hay \(K, E, J\) thẳng hàng. Kết thúc chứng minh.
Bài 4
(1 điểm)
Với \(n\) nguyên, \(n \geq 3\), hãy tìm \(n\) để có thể viết các số \(1,2,3, \ldots, n^2\) vào các ô vuông của bảng \((n \times n)\) mỗi ô đúng một số, sao cho tổng 4 số trên các hình bất kỳ dạng
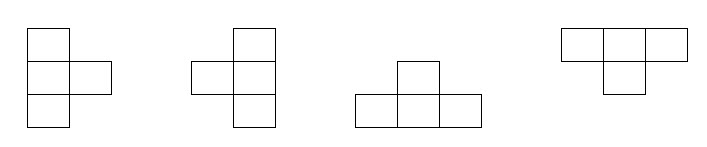
của bảng đều là số chẵn.
Cách giải 1:
Xét hình chữ thập
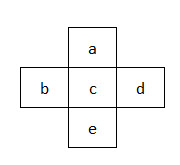
Ta có
\( (a+b+c+d)-(c+b+d+e)=(a-e) \) chẵn \(\rightarrow a, e \) cùng tính chẵn lẻ \(a \equiv e (\bmod 2) \)
\(\rightarrow a+e\) chẵn
Ta có \(a+b+c+e\) chẵn
Kết hợp hai điều trên \(\rightarrow b+c\) chẵn \(\rightarrow b \equiv c(\bmod 2)\)
Ta lại có
\[ (b+a+c+e)-(d+a+c+e)=b-d \text { chån } \rightarrow b \equiv d \quad(\bmod 2) \]
\(\rightarrow b+d\) chẵn.
Ta có \(a+b+c+d\) chẵn.
Kết hợp hai điều trên \(\rightarrow a+c\) chẵn \(\rightarrow a \equiv c(\bmod 2)\).
Tóm lại
\[ a \equiv e \equiv c \equiv b \equiv d \quad(\bmod 2) \] 5 số trong hình chữ thập cùng tính chẵn lẻ
- Xét liên tiếp các hình chữ thập để kề nhau
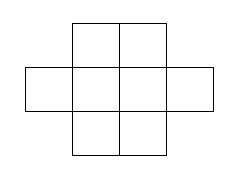
Suy ra tất cả các ô trong (trừ 4 ô góc) cùng tính chẵn lẻ.
Xét \(n \geq 4\), ta có \(n^2 \geq 16 \rightarrow\) có \(\geq 8\) ô chứa số chẵn hoặc \(\geq 8\) ô chứa số lẻ.
Vi có \(\geq 8\) ô chứa số chån \(\rightarrow\) tồn tại 1 ô trong chứa số chẵn
\(\rightarrow\) Tất cả các ô đều chứa số chån \(\rightarrow\) số ô chứa số lẻ \(\leq 4\) (ô góc) (Mâu thuẫn) \(\rightarrow\) Không xếp dược.
Với \(n=3\) thỏa mãn với cách xếp sau
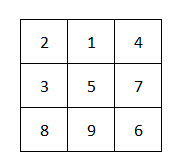
Đáp số \(n=3\).